Solve the given game tree using min max algorithm.

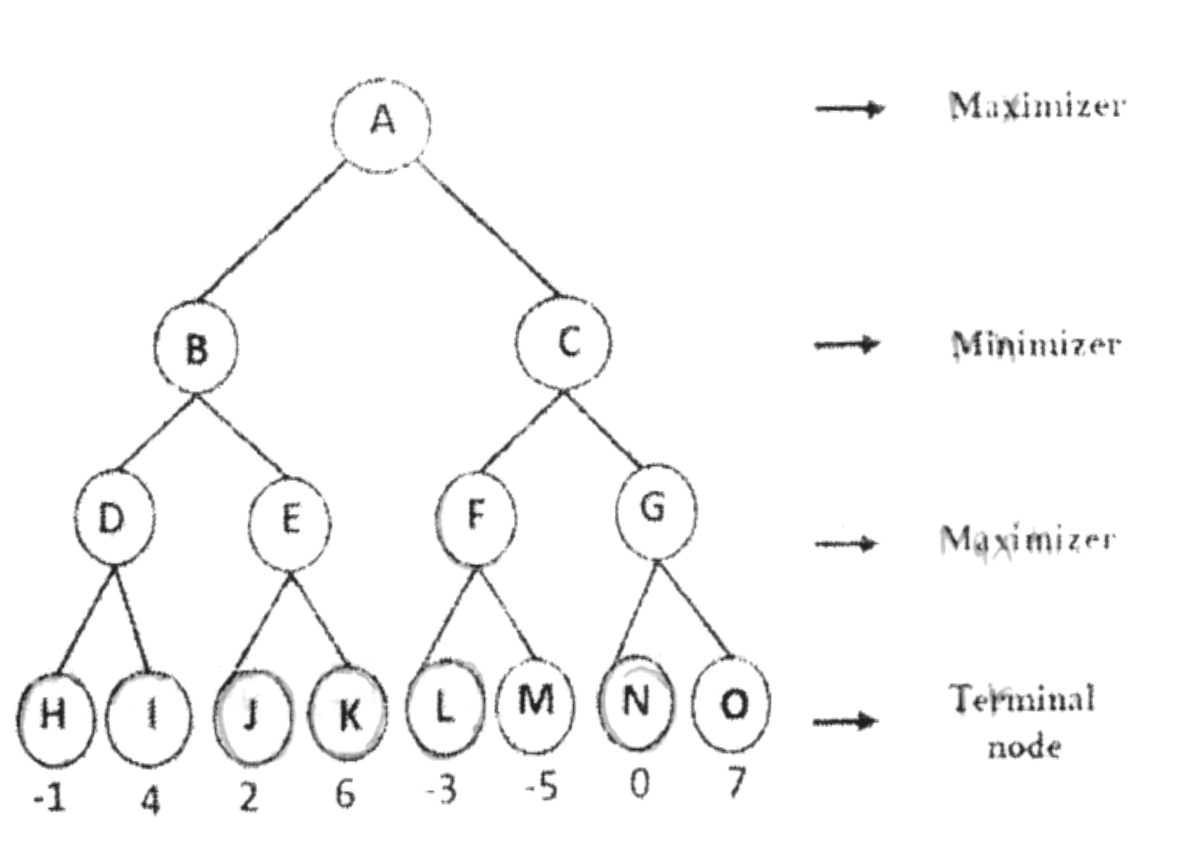
Step-by-Step Minimax Algorithm

Tree Levels:

• Level 1 (Root Node): Maximizer (A)
• Level 2: Minimizer (B, C)
• Level 3: Maximizer (D, E, F, G)
• Level 4 (Leaf Nodes): Terminal nodes with values

Terminal Node Values:

• ( H = -1 )
• ( I = 4 )
• ( J = 2 )
• ( K = 6 )
• ( L = -3 )
• ( M = -5 )
• ( N = 0 )
• ( O = 7 )

Step 1: Evaluate Leaf Nodes (Level 4)

Step 2: Propagate Values to Level 3 (Maximizer Nodes D, E, F, G)

1. Node D:

   • Children: H (-1), I (4)
   • Value of D: (\max(-1, 4) = 4)

2. Node E:

   • Children: J (2), K (6)
   • Value of E: (\max(2, 6) = 6)

3. Node F:

   • Children: L (-3), M (-5)
   • Value of F: (\max(-3, -5) = -3)

4. Node G:

   • Children: N (0), O (7)
   • Value of G: (\max(0, 7) = 7)

Step 3: Propagate Values to Level 2 (Minimizer Nodes B, C)

1. Node B:

   • Children: D (4), E (6)
   • Value of B: (\min(4, 6) = 4)

2. Node C:

   • Children: F (-3), G (7)
   • Value of C: (\min(-3, 7) = -3)

Step 4: Propagate Values to Level 1 (Maximizer Node A)

1. Node A:
   • Children: B (4), C (-3)
   • Value of A: (\max(4, -3) = 4)

Result:

The optimal value for the root node (A) using the Minimax algorithm is 4. Therefore, the best move for the maximizer at node A is to follow the path leading through node B.

Propagated Values in the Tree:

            A (4)
           /   \
        B (4)   C (-3)
        /       /
      D (4)    F (-3)   G (7)
      / \      / \      / \
   H(-1) I(4) L(-3) M(-5) N(0) O(7)
            E (6)
           /   \
        J(2)  K(6)

This solution demonstrates how the Minimax algorithm is used to determine the optimal move for a player, ensuring that the chosen strategy minimizes the maximum possible loss.