Stochastic Update and Simulated Annealing

Definition

Stochastic Update: A method in which the state of a system or the values of variables are updated probabilistically rather than deterministically. This approach is used in various optimisation algorithms to explore the search space more thoroughly.

Simulated Annealing (SA): A probabilistic optimisation algorithm inspired by the annealing process in metallurgy. It is used to find an approximate global optimum in a large search space by iteratively exploring solutions and allowing occasional steps to worse solutions to escape local optima.

Key Concepts

1. Stochastic Update:

   • Probability Distribution: Determines the likelihood of each possible update.
   • Randomness: Introduced to avoid getting stuck in local optima.
   • Markov Chain: A sequence of possible updates where the next state depends only on the current state.

2. Simulated Annealing:

   • Annealing Process: A physical process involving heating and controlled cooling of a material to remove defects and optimize its structure.
   • Objective Function: The function that needs to be minimized or maximized in the optimization problem.
   • Temperature: A parameter controlling the probability of accepting worse solutions, analogous to the temperature in physical annealing.
   • Cooling Schedule: A plan for gradually reducing the temperature during the optimization process.
   • Acceptance Probability: The probability of accepting a worse solution, which decreases as the temperature decreases.

Detailed Explanation

Stochastic Update

Stochastic updates introduce randomness into the process of updating system states or variable values. This approach is essential in various optimization and learning algorithms to ensure comprehensive exploration of the solution space and to prevent premature convergence to local optima.

Components:

• Random Sampling: States or variables are updated based on samples drawn from a probability distribution.
• Transition Probability: The probability of moving from one state to another is determined by a predefined probability distribution.
• Markov Property: The next state depends only on the current state and not on the sequence of states that preceded it.

Applications:

• Genetic Algorithms: Use stochastic updates to generate new solutions through mutation and crossover.
• Monte Carlo Methods: Rely on stochastic sampling to approximate complex integrals and distributions.
• Stochastic Gradient Descent: Updates the weights of neural networks probabilistically to optimize the loss function.

Simulated Annealing

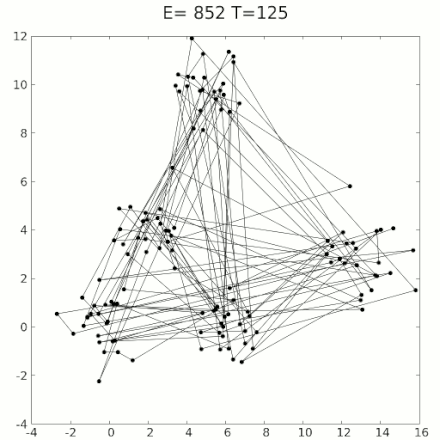
Simulated Annealing is an optimization technique that mimics the physical process of annealing. It aims to find a global minimum of an objective function by allowing probabilistic transitions to worse solutions, which helps escape local minima.

Algorithm Steps:

1. Initialization: Start with an initial solution ( S_0 ) and an initial temperature ( T_0 ).
2. Iteration:
   • Generate Neighbor: Generate a neighboring solution ( S' ) from the current solution ( S ).
   • Objective Function Evaluation: Evaluate the objective function ( f(S') ) and ( f(S) ).
   • Acceptance Criterion: If ( f(S') ) is better than ( f(S) ), accept ( S' ). If ( f(S') ) is worse, accept ( S' ) with a probability ( P = \exp\left(\frac{f(S) - f(S')}{T}\right) ).
   • Update: Update the current solution to ( S' ) and reduce the temperature according to the cooling schedule.
3. Termination: Repeat the iteration until the system is "frozen," i.e., no further significant changes occur or a maximum number of iterations is reached.

Cooling Schedule: The cooling schedule determines how the temperature is reduced over time. Common schedules include:

• Linear: ( T = T_0 - k \cdot \text{iteration} )
• Geometric: ( T = T_0 \cdot \alpha^{\text{iteration}} ) (with ( 0 < \alpha < 1 ))
• Logarithmic: ( T = \frac{T_0}{\log(1 + \text{iteration})} )

Acceptance Probability:

• At high temperatures, the probability of accepting worse solutions is high, allowing the algorithm to explore the search space widely.
• As the temperature decreases, the acceptance probability decreases, focusing the search on the local area around the best solutions found.

Applications:

• Traveling Salesman Problem: Finding the shortest possible route that visits a set of cities and returns to the origin city.
• Scheduling: Optimizing job schedules to minimize total completion time or maximize resource utilization.
• Function Optimization: Finding the global minimum or maximum of complex, multimodal functions.

Diagrams

• 
• 
• 

Links to Resources

• Simulated Annealing Wikipedia
• GeeksforGeeks on Simulated Annealing
• Stochastic Update Wikipedia

Notes and Annotations

• Summary of key points:

  • Stochastic updates introduce randomness into the update process to explore the search space and avoid local optima.
  • Simulated Annealing is a probabilistic optimization algorithm that uses a temperature parameter to control the acceptance of worse solutions, facilitating the escape from local minima and aiming for the global minimum.

• Personal annotations and insights:

  • Stochastic updates are crucial in optimization algorithms to prevent getting stuck in local optima and ensure a thorough search of the solution space.
  • Simulated Annealing's strength lies in its ability to mimic the annealing process, allowing it to find near-optimal solutions in complex search spaces.
  • Understanding the principles of stochastic updates and Simulated Annealing provides a foundation for developing robust optimization techniques applicable to a wide range of practical problems.
  • Real-world applications of Simulated Annealing demonstrate its versatility and effectiveness in solving complex optimization problems, such as the traveling salesman problem and scheduling tasks.

Backlinks

• Linked from Unit III Associative LearningUnit III Associative LearningOverview Associative learning is the focus of this unit, which begins with an introduction to the concept and its significance in neural networks. You'll study Hopfield networks and their error performance, as well as simulated annealing processes. The unit covers Boltzmann machines and Boltzmann learning, including state transition diagrams and the problem of false minima. Stochastic update methods and simulated annealing are also discussed. Finally, the unit explores basic functional units of