SOM Algorithm

Definition

The Self-Organizing Map (SOM) algorithm, developed by Teuvo Kohonen, is an unsupervised learning algorithm that produces a low-dimensional (typically 2D) representation of a higher-dimensional input space. It is used for clustering, visualisation, and dimensionality reduction, preserving the topological properties of the input data.

Key Concepts

• Unsupervised LearningUnsupervised LearningUnsupervised Learning Definition Unsupervised Learning is a type of machine learning where the algorithm is trained on unlabeled data. The goal is to infer the natural structure present within a set of data points. Unlike supervised learning, there are no predefined labels or outcomes, and the system tries to learn the patterns and the structure from the data. Key Concepts Unlabeled Data:** Data that does not have associated labels or target values. Clustering:** Grouping a set of objects in: The SOM algorithm learns to classify data without the need for labeled inputs.
• Topology Preservation: The algorithm maps high-dimensional input data onto a lower-dimensional grid while maintaining the spatial relationships of the input data.
• Competitive Learning: Neurons in the SOM compete to represent the input data, with only the winning neuron and its neighbors being updated.
• Neighbourhood Function: Defines the region around the winning neuron that gets updated, promoting smooth transitions across the map.
• Dimensionality Reduction: Transforms high-dimensional data into a lower-dimensional space for easier visualization and analysis.

Detailed Explanation

Initialization

• Weight Initialization: The weight vectors of the neurons are typically initialized with small random values. Alternatively, they can be initialized with samples from the input data or linearly.

Competition

• Best Matching Unit (BMU): For each input vector, the neuron with the closest weight vector (measured by Euclidean distance) is identified as the BMU. The Euclidean distance is calculated as follows: [ \text{Distance} = |\mathbf{x} - \mathbf{w}_i| ] where ( \mathbf{x} ) is the input vector and ( \mathbf{w}_i ) is the weight vector of neuron ( i ).

Adaptation

• Updating Weights: The weights of the BMU and its neighbors are updated to make them more similar to the input vector. The update rule is: [ \mathbf{w}_i(t+1) = \mathbf{w}i(t) + \eta(t) h{ci}(t) (\mathbf{x} - \mathbf{w}i(t)) ] where ( \eta(t) ) is the learning rate, ( h{ci}(t) ) is the neighborhood function, ( \mathbf{x} ) is the input vector, and ( \mathbf{w}_i(t) ) is the weight vector at time ( t ).

Neighborhood Function

• Neighborhood Function: Defines the influence of the BMU on its neighbors. A common choice is the Gaussian function: [ h_{ci}(t) = \exp\left(-\frac{|r_c - r_i|^2}{2\sigma(t)^2}\right) ] where ( r_c ) and ( r_i ) are the positions of the BMU and neuron ( i ) on the map, and ( \sigma(t) ) is the neighborhood radius, which decreases over time.

Iteration

• Repeating the Process: The steps of finding the BMU and updating the weights are repeated for a specified number of iterations or until convergence. The learning rate ( \eta(t) ) and neighborhood radius ( \sigma(t) ) decrease over time to fine-tune the map.

Diagrams

Basic Structure of a Self-Organizing Map

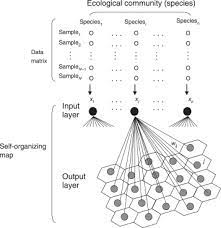
Training Process in SOM

Links to Resources

• Self-Organizing Maps by Teuvo Kohonen: Comprehensive resource on SOMs, authored by the creator of the method.
• Introduction to Self-Organizing Maps: An accessible introduction to SOMs with examples and applications.
• Neural Networks and Learning Machines by Simon Haykin: Textbook providing in-depth coverage of SOMs and other neural network models.

Notes and Annotations

• Summary of Key Points:
  • SOMs use unsupervised learning to map high-dimensional data onto a lower-dimensional grid.
  • The algorithm preserves the topological properties of the input space, making it useful for clustering and visualization.
  • Key steps include initialization, competition, adaptation, and iteration, with a decreasing neighborhood function and learning rate over time.
• Personal Annotations and Insights:
  • SOMs are particularly effective for exploratory data analysis, as they can reveal hidden patterns and structures in complex datasets.
  • The neighborhood function ensures that the map evolves smoothly, allowing for meaningful visualizations of high-dimensional data.

Backlinks

• Pattern Clustering and Feature Mapping Network: Refer to notes on pattern clustering and feature mapping for a broader understanding of unsupervised learning networks.
• Unsupervised Learning Techniques: Connect to discussions on various unsupervised learning methods and their applications.
• Neural Network Models Overview: Link to an overview of different neural network models to see where SOM fits in the landscape of machine learning techniques.