Pattern Clustering and Feature Mapping Network

Definition

Pattern Clustering and Feature Mapping Network, also known as Self-Organizing Map (SOM), is a type of Unsupervised LearningUnsupervised LearningUnsupervised Learning Definition Unsupervised Learning is a type of machine learning where the algorithm is trained on unlabeled data. The goal is to infer the natural structure present within a set of data points. Unlike supervised learning, there are no predefined labels or outcomes, and the system tries to learn the patterns and the structure from the data. Key Concepts Unlabeled Data:** Data that does not have associated labels or target values. Clustering:** Grouping a set of objects in network that performs clustering and feature mapping. Developed by Teuvo Kohonen, SOM organizes high-dimensional data into a low-dimensional (typically 2D) grid, preserving the topological properties of the input space.

Key Concepts

• Self-Organisation: The network learns to organise itself based on the input patterns without supervision.
• Topology Preservation: The mapping from high-dimensional input space to low-dimensional map maintains the spatial relationships of the data.
• Neighbourhood Function: The update of weights affects not only the winning neuron but also its neighbours, promoting smooth transitions across the map.
• Dimensionality Reduction: The high-dimensional data is represented in a lower-dimensional space for easier visualisation and interpretation.

Detailed Explanation

• Self-Organization Process: When an input vector is presented, each neuron computes a similarity measure (e.g., Euclidean distance) to determine the winning neuron (Best Matching Unit, BMU). The weights of the BMU and its neighbors are then updated to become more similar to the input vector.
• Learning Algorithm:
  1. Initialization: Initialize the weights of the neurons.
  2. Sampling: Randomly select an input vector from the dataset.
  3. Best Matching Unit (BMU): Find the neuron whose weight vector is closest to the input vector.
  4. Updating: Adjust the weights of the BMU and its neighboring neurons: [ \mathbf{w}_i(t+1) = \mathbf{w}i(t) + \eta(t) h{ci}(t) (\mathbf{x} - \mathbf{w}_i(t)) ] where ( \mathbf{w}i(t) ) is the weight vector of neuron ( i ) at time ( t ), ( \eta(t) ) is the learning rate, ( h{ci}(t) ) is the neighborhood function centered on the BMU, and ( \mathbf{x} ) is the input vector.
  5. Neighborhood Function: Typically a Gaussian function that decreases over time and distance from the BMU.
  6. Iteration: Repeat steps 2-5 for a specified number of iterations or until convergence.
• Topology Preservation: Ensures that similar input patterns map to nearby neurons on the map, maintaining the spatial relationships of the data.

Diagrams

Basic Structure of a Self-Organizing Map

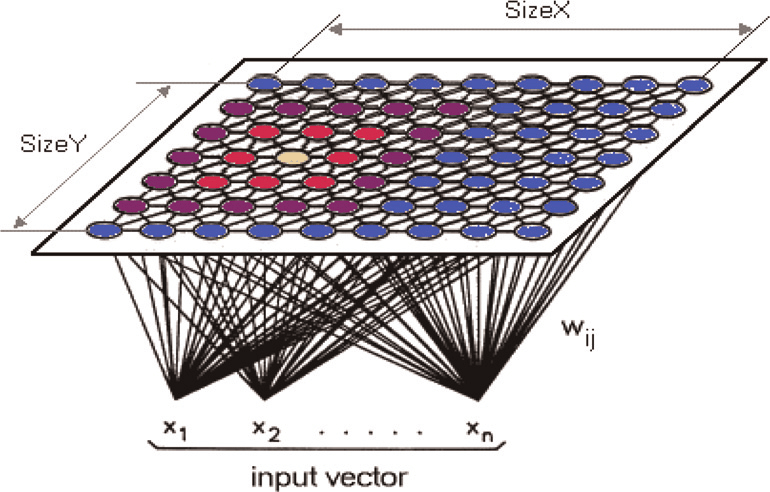
Weight Update Process in SOM

Links to Resources

• Self-Organizing Maps by Teuvo Kohonen: Comprehensive resource on SOMs, authored by the creator of the method.
• Introduction to Self-Organizing Maps: An accessible introduction to SOMs with examples and applications.
• Neural Networks and Learning Machines by Simon Haykin: Textbook providing in-depth coverage of SOMs and other neural network models.

Notes and Annotations

• Summary of Key Points:
  • SOMs are used for pattern clustering and feature mapping in an unsupervised manner.
  • The network self-organizes based on input patterns, preserving the topological relationships.
  • Weight updates affect the BMU and its neighbors, promoting a smooth and continuous mapping.
• Personal Annotations and Insights:
  • SOMs are particularly useful for visualizing high-dimensional data in a low-dimensional space.
  • The topology preservation feature makes SOMs suitable for applications requiring spatial awareness, such as image and speech recognition.

Backlinks

• Competitive Learning Networks: Refer to notes on competitive learning networks for foundational concepts that underpin the operation of SOMs.
• Unsupervised Learning Techniques: Connect to broader discussions on unsupervised learning methods and their applications.
• Dimensionality Reduction Techniques: Link to notes on other dimensionality reduction methods for comparative understanding.