My Blog.

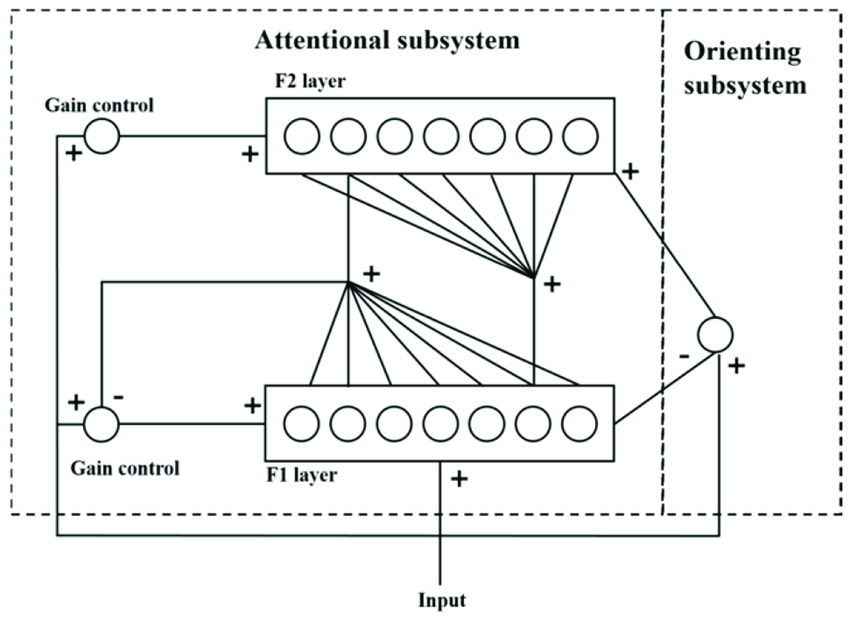
Draw the network architecture of ART network. Explain the algorithm for designing the weights of ART network.

Network Architecture of the ART (Adaptive Resonance Theory) Network

The ART network consists of two primary layers: the Comparison Layer (F1) and the Recognition Layer (F2), connected by bottom-up and top-down weights. Below is a diagram representing the basic architecture of an ART network:

           +---------------------+
           |      F2 Layer       |
           | (Recognition Layer) |
           +---------+-----------+
                     |
      Bottom-Up      |    Top-Down
        Weights      |     Weights
            (W)      |       (T)
                     |
           +---------+-----------+
           |      F1 Layer       |
           |  (Comparison Layer) |
           +---------+-----------+
                     |
                Input Vector

Components:

  1. Input Layer: Represents the input vector.
  2. F1 Layer (Comparison Layer): Receives and preprocesses the input vector.
  3. F2 Layer (Recognition Layer): Contains neurons that represent different categories or clusters.
  4. Bottom-Up Weights (W): Connects F1 to F2 and determines how input features influence the activation of the F2 neurons.
  5. Top-Down Weights (T): Connects F2 to F1 and represents the expectation of the category for comparison with the input pattern.

Algorithm for Designing the Weights of the ART Network

The weight design algorithm in the ART network involves initial setup and iterative learning based on input patterns and the vigilance parameter.

Initialization

  1. Weight Initialization:
    • Initialize bottom-up weights ( W ) and top-down weights ( T ) with small random values or values derived from initial training data.
    • Example for a network with ( n ) input neurons and ( m ) output neurons: [ W_{ij} = \text{random small value}, \quad T_{ji} = \text{random small value} ] where ( W_{ij} ) is the weight from input neuron ( i ) to output neuron ( j ), and ( T_{ji} ) is the weight from output neuron ( j ) to input neuron ( i ).

Learning Algorithm

  1. Input Presentation:

    • Present an input vector ( \mathbf{x} ) to the F1 layer.

  2. Compute Activation:

    • Calculate the activation of each neuron in the F2 layer based on the bottom-up weights ( W ). Commonly, this is done using the dot product: [ T_j = \mathbf{x} \cdot \mathbf{w}j = \sum{i} x_i W_{ij} ] where ( \mathbf{w}_j ) is the weight vector of the ( j )-th neuron in the F2 layer.

  3. Choose the Winning Neuron:

    • Identify the neuron in the F2 layer with the highest activation ( T_j ). This neuron is the candidate for representing the input pattern. [ J = \arg\max_j T_j ]

  4. Vigilance Test:

    • Compare the similarity between the input vector and the top-down weight vector ( \mathbf{t}_J ) of the winning neuron ( J ). The similarity is often measured as the normalized dot product: [ \frac{| \mathbf{x} \cap \mathbf{t}_J |}{| \mathbf{x} |} \geq \rho ] where ( \rho ) is the vigilance parameter, and ( | \mathbf{x} \cap \mathbf{t}_J | ) is the intersection of ( \mathbf{x} ) and ( \mathbf{t}_J ).

  5. Resonance and Learning:

    • If the vigilance test is satisfied (i.e., the similarity exceeds the vigilance parameter ( \rho )), the network enters a resonance state, and learning occurs:
      • Update the bottom-up weights ( W ) and the top-down weights ( T ) of the winning neuron ( J ): [ W_{ij} = \frac{x_i}{\sum_{k} x_k}, \quad T_{ji} = x_i ]
    • If the vigilance test is not satisfied, inhibit the current winning neuron and repeat the process with the next highest activation neuron.

  6. Repeat:

    • Repeat the input presentation and learning steps for each input vector until all patterns are learned or a stopping criterion is met.

Example of Weight Update

Assume we have the following input vector and initial weights:

  • Input vector: (\mathbf{x} = [1, 1, 0, 0])
  • Initial bottom-up weights for neuron ( j ): ( \mathbf{w}_j = [0.1, 0.1, 0.1, 0.1] )
  • Initial top-down weights for neuron ( j ): ( \mathbf{t}_j = [0.1, 0.1, 0.1, 0.1] )
  • Vigilance parameter: (\rho = 0.5)

Step-by-Step Process:

  1. Compute Activation: [ T_j = 1 \cdot 0.1 + 1 \cdot 0.1 + 0 \cdot 0.1 + 0 \cdot 0.1 = 0.2 ]

  2. Vigilance Test: [ \frac{| [1, 1, 0, 0] \cap [0.1, 0.1, 0.1, 0.1] |}{| [1, 1, 0, 0] |} = \frac{0.2}{2} = 0.1 < 0.5 ]

    • The test fails, so we proceed to the next neuron or create a new cluster if all neurons fail.

  3. Update Weights:

    • For a new neuron or the winning neuron (if test passes), update weights: [ W_{ij} = \frac{x_i}{\sum_{k} x_k} = \frac{1}{2}, \quad T_{ji} = x_i = 1 ]

Conclusion

The ART network architecture and its learning algorithm are designed to balance stability and plasticity, enabling the network to learn new patterns without forgetting old ones. The key components include the input layer, comparison layer (F1), recognition layer (F2), and the weight vectors (W and T). The learning algorithm involves initializing the weights, presenting input vectors, computing activations, performing vigilance tests, and updating the weights iteratively. This process results in effective clustering and pattern recognition.

Pasted image 20240520225558.png