ART Networks

Definition

Adaptive Resonance Theory (ART) Networks are a type of neural network developed by Stephen Grossberg that is designed to solve the stability-plasticity dilemma, which refers to the challenge of learning new information without forgetting previously learned information. ART networks are capable of incremental learning, pattern recognition, and clustering in a stable and consistent manner.

Key Concepts

• Stability-Plasticity Dilemma: The balance between learning new patterns (plasticity) and retaining existing patterns (stability).
• Resonance: The state where the network's response to an input is sufficiently similar to an existing memory, leading to learning.
• Vigilance Parameter: Controls the level of similarity required for resonance, affecting how the network handles new patterns.
• Fast Learning: Quick adaptation to new patterns when they do not resonate with existing memories.
• Slow Learning: Gradual adjustment of weights during resonance to refine pattern recognition.

Detailed Explanation

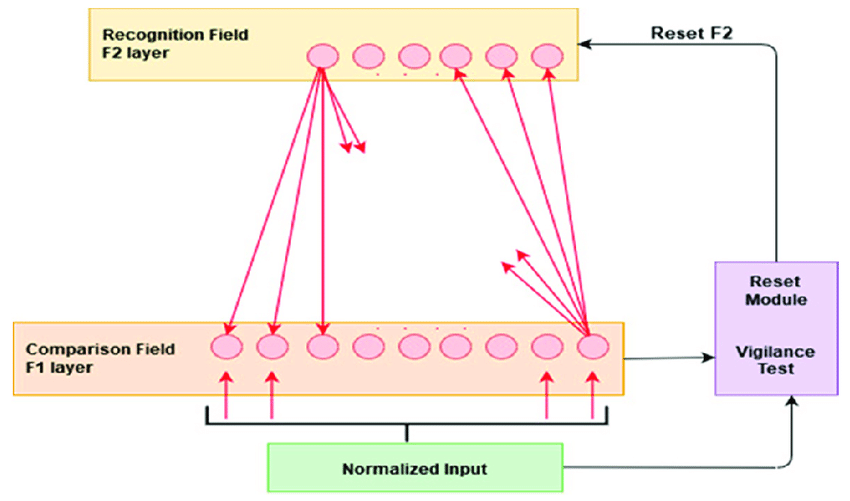
• Network Architecture: An ART network typically consists of two layers:
  • Comparison Layer (F1): Receives input patterns and processes them.
  • Recognition Layer (F2): Contains memory traces of learned patterns and outputs the recognised pattern.
• Resonance Process:
  1. Input Presentation: An input vector is presented to the F1 layer.
  2. Pattern Matching: The input is compared with the weight vectors in the F2 layer to find a close match.
  3. Vigilance Test: The similarity between the input and the matched pattern is checked against the vigilance parameter.
  4. Resonance or Reset: If the similarity exceeds the vigilance threshold, resonance occurs, and the pattern is learned or reinforced. If not, the network resets, and another pattern match is attempted.
• Learning Rule: During resonance, the weights are updated to better match the input pattern: [$$ \mathbf{w}_i(t+1) = (1 - \alpha)\mathbf{w}_i(t) + \alpha\mathbf{x} $$] where ( \mathbf{w}_i(t) ) is the weight vector at time ( t ), ( \alpha ) is the learning rate, and ( \mathbf{x} ) is the input vector.

Diagrams

Basic Structure of an ART Network

Resonance and Vigilance Mechanism

Links to Resources

• Adaptive Resonance Theory (ART) Overview: Detailed reference entry on ART networks, explaining their principles and applications.
• ART Network Tutorial: An accessible tutorial on ART networks with examples and practical insights.
• Neural Networks and Learning Machines by Simon Haykin: Textbook providing an in-depth discussion on ART networks and other neural network models.

Notes and Annotations

• Summary of Key Points:
  • ART networks address the stability-plasticity dilemma, allowing for incremental learning.
  • Resonance and the vigilance parameter are crucial for controlling learning and memory.
  • Fast learning adapts to new patterns quickly, while slow learning refines existing patterns.
• Personal Annotations and Insights:
  • ART networks are highly suitable for applications requiring stable yet adaptive learning, such as real-time pattern recognition and classification tasks.
  • The adjustable vigilance parameter provides flexibility in handling noise and novel patterns, making ART networks versatile in dynamic environments.

Backlinks

• Unsupervised Learning Techniques: Refer to broader discussions on unsupervised learning methods to understand the context of ART networks.
• Competitive Learning Networks: Connect to notes on competitive learning networks for a comparative perspective on different unsupervised learning strategies.
• Neural Network Models Overview: Link to an overview of various neural network models to see where ART networks fit in the landscape of machine learning techniques.